说起迷宫想必大家都很熟悉,个人感觉迷宫对人的方向感是很大的考验,至少我的方向感是不好的,尤其是在三维空间中。由于这段时间帮导师做项目用到了三维作图,便心血来潮想做个三维迷宫玩玩。要想画出三维的迷宫游戏,我们需要先从二维开始。
二维迷宫:
迷宫的程序描述:
现实生活中,我们经常将问题用数学的方法来描述并解决(数学建模)。同样的,我们想用程序来解决问题,就得把问题程序化。废话不多说,进入正题:
我们可以用一个矩阵matrix来描绘整个迷宫:元素为1,代表是空的,元素为0代表墙。为了描述问题的方便,下面都采用9行9列的矩阵来说明问题,并且假设(0,0)为入口,(1,1)为出口。
网上也有一些常见的迷宫程序,但是它们都有一种特点,就是生成的迷宫可能没有从入口到出口的可达路径(可以通过循环来生成迷宫,直到有可达路径),或则从入口到出口有几条可达路径(如果想要只有唯一可达路径,就不行了)。这些算法大多数是通过随机数来产生迷宫矩阵matrix(随机产生0,1元素),然后通过迭代、回溯算法来找入口到出口的路径。由于矩阵matrix是随机的,这就不能保证入口到出口是可达的,这就是导致上面问题。
算法思想:
想必大家都学过树(关于树的相关操作可以看我之前的文章)这种数据结构,比如说树的遍历DFS、BFS,树的深度等等操作。当然树的类型也有很多,如完全二叉树、红黑树、B树等等。但是我现在要说的不是这些,而是另一个我发现的性质:一个节点到另一个节点的路径有且只有一条! 现在就能和前面我说的那个问题联系起来了。下面看看是怎么联系的:
我们首先将整个矩阵matrix的元素初始化为0即认为全都是墙,我们的任务就是拆墙(使元素等于1)来构成迷宫。怎么拆墙是我们算法的关键!
首先,我们随便在矩阵中找一个初始点A(4,4),将该点的值设为1,即将该点的墙拆掉。
然后,产生一个0到3的随机整数randnum(0,1,2,3分布代表上下左右四个方向),在随机数randnum表示的方向进行拆墙(注意是连拆两块),如果该方向上与目前位置隔一块的位置没有墙,就不能拆,则需要再产生随机数,在其他方向上拆墙。(注意拆墙的前提是该方向隔一块的位置是墙)
最后,在上一步骤中,一直循环,直到当前位置四个方向的隔一块的位置都没有墙可拆,就进行回溯(回退到当前位置的上一个位置),然后进行上一步骤的操作,直至没有墙可拆!
我一直相信图像是比文字更能说话的,下面我们用图像来说明上述步骤:
在强调一下:我们举例都采用9行9列的矩阵,初始点为(4,4)。
- 最开始时,只有初始点处的墙被拆掉
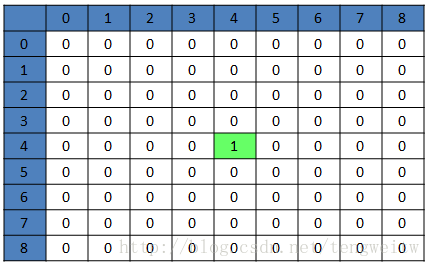
随机数randnum=2,开始向左边拆墙,由于(4,2)为0(有墙),可以拆,于是拆掉(4,2)、(4,3)位置的墙,则结果如下:
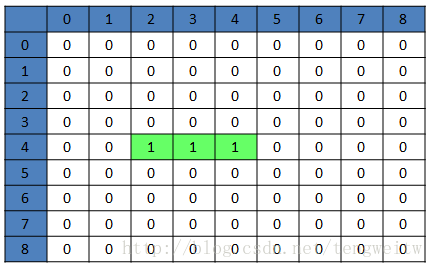
接着产生随机数randnum=1,开始向下拆墙,由于(6,2)为0(有墙),可以拆,于是拆掉(5,2)、(6,2)位置的墙,结果如下:
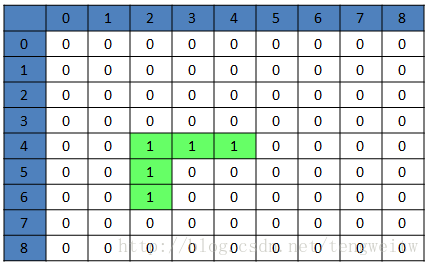
- 继续产生随机数randnum=0,开始向上拆墙,由于(4,2)为1没有墙,不可以拆,于是重新产生随机数,结果与上一张图一样:
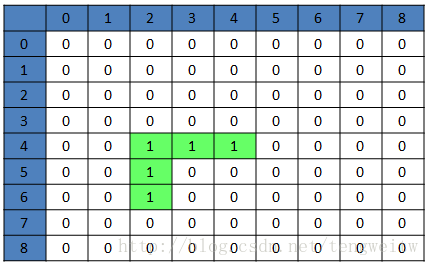
- 继续产生随机数randnum=3,开始向右拆墙,由于(6,4)为0有墙,可以拆,于是拆掉(6,3)、(6,4)位置的墙,结果如下:
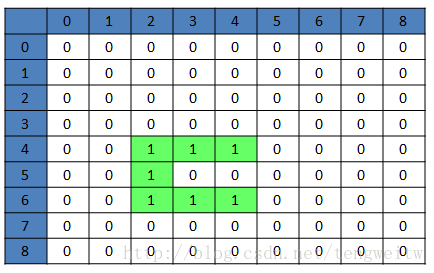
按照上述步骤重复下去,最终得到一个可能的迷宫矩阵如下:
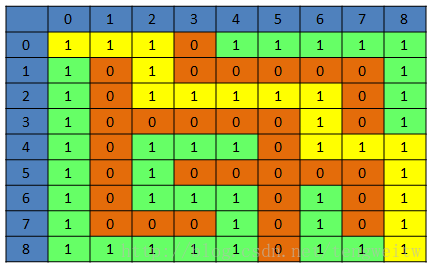
注意事项:
1、迷宫矩阵的行和列必须为基数,初始点的位置必须为偶数。(这是由算法决定的,因为算法总是从初始点出发,步长为2,到达入口点和出口点,所以初始点与入口点、出口点的横纵坐标的距离都应该是步长2的倍数)。
2、初始点的选择最好在矩阵的中间位置,可以这样想象:算法的本质就是从初始点出发到达其他点,中间会产生分支(回溯的原因,如果回溯到初始点,则是在初始点就产生分支)到达其它点(包括入口点和出口点)。因此我们可以描述成一棵树,而初始点便是树的根节点。为了更快的找到出口点与入口点的可达路径,应使树的深度较小,这样就应该将初始点选在中间位置。
3、在进行判断时,为什么要选择看隔一块是否是墙,而不是相邻块、或则隔几块?因为隔一块的话,路与墙的宽度就一样了(取相邻块或则隔几块的情况大家可以实验推导一下!)
上面我用图文并茂的方法讲述了如何生成迷宫,下面我们来看看如何生成入口到出口的可达路径:
如上一张图所示,黄色部分就是可达路径(是唯一一条),由于迷宫较小,我们可以一眼看出,当迷宫较大时,我们就要靠矩阵来计算了。在上面的迷宫生成算法中,我们可以在拆墙的时候来记录节点,则当拆到入口时,便记录了从初始点到入口的路径,同理,我们也可以得到初始点到出口的路径,这样根据这两条路径就很容易得到入口到出口的路径了。前面我也说过,整个算法就是生成树的过程,其中初始点为根节点,找到可达路径相当于找到树中入口节点到出口节点的路径。前面我也提到,该树中任意两个节点的可达路径是唯一的,所以该算法生成的迷宫的入口到出口的路径是唯一的。
至此,我们已经讲述了整个的算法思想和流程,下面给出源代码(c++,vs2010实现),源文件给出了详细的注释,就不过多解释。程序总共5个文件:1、Maze.h 2、Maze.cpp 3、MazeStack.h 4、MazeStack.cpp 5、main.cpp。具体内容如下:
1、Maze.h
Maze.h 源代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| #include<iostream>
#include<ctime>
#include<vector>
#define M 9
#define N 9
using namespace std;
class MazeStack;
class Maze//定义迷宫节点信息。
{
public:
int i;
int j;
int state;
};
class MazeMat
{
Maze matrix[M][N];
vector<Maze> EntryPath;
vector<Maze> ExitPath;
vector<Maze> FinalPath;
MazeStack *mazeStack;
public:
void initMaze();
void createMaze();
void displayMaze();
void FindWay();
};
|
2、Maze.cpp
Maze.cpp 源代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
| #include"MazeStack.h"
using namespace std;
void MazeMat::initMaze()
{
for(int i=0;i<M;i++)
for(int j=0;j<N;j++)
{
matrix[i][j].i=i;
matrix[i][j].j=j;
matrix[i][j].state=0;
}
mazeStack=new MazeStack();
EntryPath.clear();
ExitPath.clear();
FinalPath.clear();
}
void MazeMat::createMaze()
{
int i=4;
int j=4;
bool Left=false;
bool Right=false;
bool Up=false;
bool Down=false;
matrix[i][j].state=1;
srand((int)time(0));
Maze temp;
temp.i=i;
temp.j=j;
temp.state=0;
int count1=0;
int num1=0;
mazeStack->Push(temp);
while(1)
{
temp.i=i;
temp.j=j;
int randNum=0;
randNum=rand()%4;
if(temp.i==0&&temp.j==0)
{
EntryPath.clear();
while(mazeStack->isEmpty() == false)
{
EntryPath.push_back(mazeStack->GetTop());
mazeStack->Pop();
}
for(int ii=EntryPath.size()-1;ii>=0;ii--)
{
mazeStack->Push(EntryPath[ii]);
}
}
if(temp.i==M-1&&temp.j==N-1)
{
ExitPath.clear();
while(mazeStack->isEmpty() == false)
{
ExitPath.push_back(mazeStack->GetTop());
mazeStack->Pop();
}
for(int i=ExitPath.size()-1;i>=0;i--)
{
mazeStack->Push(ExitPath[i]);
}
}
switch(randNum)
{
case 0:
if(Up==false&&i>1&&matrix[i-2][j].state!=1)
{
mazeStack->Push(temp);
matrix[i-1][j].state=1;
matrix[i-2][j].state=1;
i=i-2;
Left=false;
Right=false;
Up=false;
Down=false;
}
else
Up=true;
break;
case 1:
if(Down==false&&i<M-2&&matrix[i+2][j].state!=1)
{
mazeStack->Push(temp);
matrix[i+1][j].state=1;
matrix[i+2][j].state=1;
i=i+2;
Left=false;
Right=false;
Up=false;
Down=false;
}
else
Down=true;
break;
case 2:
if(Left==false&&j>1&&matrix[i][j-2].state!=1)
{
mazeStack->Push(temp);
matrix[i][j-1].state=1;
matrix[i][j-2].state=1;
j=j-2;
Left=false;
Right=false;
Up=false;
Down=false;
}
else
Left=true;
break;
case 3:
if(Right==false&&j<N-2&&matrix[i][j+2].state!=1)
{
mazeStack->Push(temp);
matrix[i][j+1].state=1;
matrix[i][j+2].state=1;
j=j+2;
Left=false;
Right=false;
Up=false;
Down=false;
}
else
Right=true;
break;
}
if(Left&&Right&&Up&&Down)
{
if(mazeStack->isEmpty())
{
return ;
}
else
{
i = mazeStack->GetTop().i;
j = mazeStack->GetTop().j;
mazeStack->Pop();
Left=false;
Right=false;
Up=false;
Down=false;
}
}
}
}
void MazeMat::displayMaze()
{
matrix[0][0].state = matrix[M-1][N-1].state = 2;
for(int i=0;i<FinalPath.size();i++)
{
matrix[FinalPath.at(i).i][FinalPath.at(i).j].state=3;
}
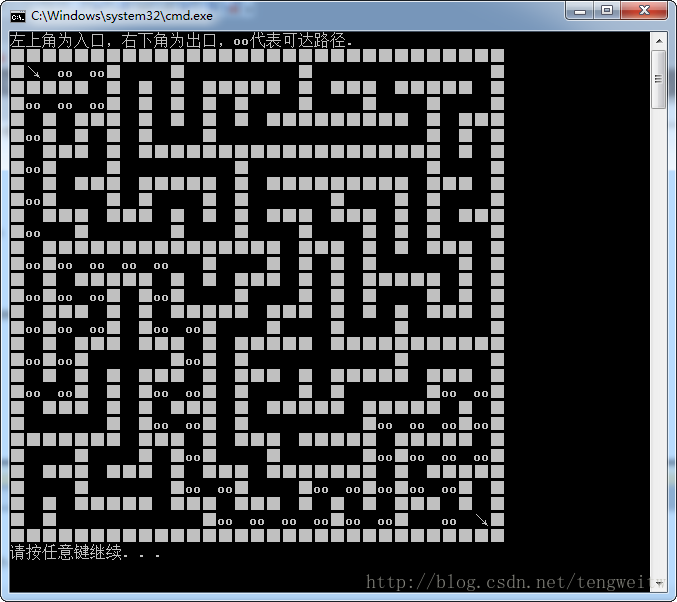
cout<<"左上角为入口,右下角为出口,oo代表可达路径."<<endl;
for(int k=0;k<N+2;k++)
cout<<"■";
cout<<endl;
for (int i = 0; i < M; i++)
{
cout<<"■";
for (int j = 0; j <N; j++)
{
switch ( matrix[i][j].state )
{
case 0:cout<<"■";break;
case 1:cout<<" ";break;
case 2:cout<<"↘";break;
case 3:cout<<"oo";break;
}
}
cout<<"■";
cout<<endl;
}
for(int k=0;k<N+2;k++)
cout<<"■";
cout<<endl;
}
void MazeMat::FindWay()
{
FinalPath.clear();
int i=0,j=0;
for(i=EntryPath.size()-1,j=ExitPath.size()-1;i>=0&&j>=0;i--,j--)
{
if(EntryPath.at(i).i!=ExitPath.at(j).i||EntryPath.at(i).j!=ExitPath.at(j).j)
{
break;
}
}
if(i<0)
{
for(int k=ExitPath.size()-EntryPath.size()-1;k>=0;k--)
{
FinalPath.push_back(ExitPath.at(k));
}
}
else if(j<0)
{
for(int k=EntryPath.size()-ExitPath.size()-1;k>=0;k--)
{
FinalPath.push_back(EntryPath.at(k));
}
}
else
{
for(int k=0;k<=i+1;k++)
{
FinalPath.push_back(EntryPath.at(k));
}
for(int k=j;k>=0;k--)
{
FinalPath.push_back(ExitPath.at(k));
}
}
}
|
3、MazeStack.h
MazeStack.h 源代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| #include"Maze.h"
typedef Maze ElementType;
typedef struct node
{
ElementType data;
struct node *next;
}Node;
class MazeStack
{
public:
MazeStack():bottom(NULL),top(NULL),Size(NULL){}
~MazeStack(){}
bool isEmpty();
bool Push(ElementType e);
ElementType GetTop();
ElementType Pop();
private:
Node *bottom;
Node *top;
int Size;
};
|
4、MazeStack.cpp
MazeStack.cpp 源代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| #include"MazeStack.h"
bool MazeStack::isEmpty()
{
if(top==bottom)
return true;
return false;
}
bool MazeStack::Push(Maze m)
{
Node *temp;
temp=top;
top=new Node();
if(!top)
return false;
top->data=m;
top->next=temp;
Size++;
return true;
}
Maze MazeStack::Pop()
{
Node temp;
temp.data=top->data;
temp.next=top->next;
delete top;
top=temp.next;
Size--;
return temp.data;
}
Maze MazeStack::GetTop()
{
return top->data;
}
|
5、main.cpp
main.cpp 源代码:
1
2
3
4
5
6
7
8
9
10
11
| #include"MazeStack.h"
void main()
{
MazeMat matrix;
matrix.initMaze();
matrix.createMaze();
matrix.FindWay();
matrix.displayMaze();
}
|
具体的程序截图如下:
1、9行9列的迷宫:
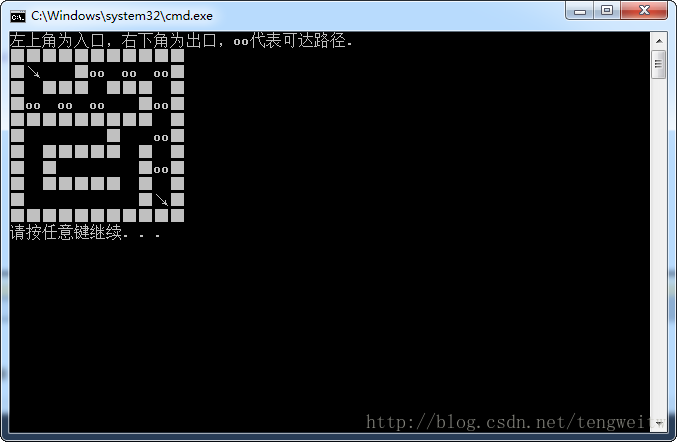
2、19行19列的迷宫:
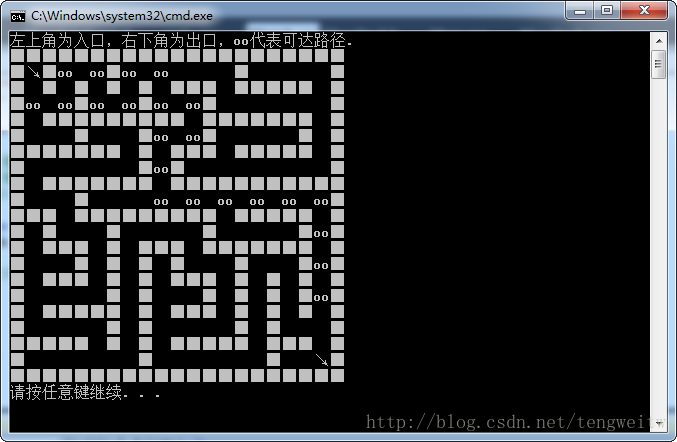
3、29行29列的迷宫:
2维到3维的转化
上面的程序实现是在二维平面上用控制台通过c++实现的,显然不够生动形象。于是我用Qt5+opengl实现了3d效果,并且可以通过鼠标操作。之所以选择Qt是因为它也是用c++编程的,所以前面写的程序几乎不用改动就可以直接运行。
编程思想:
1、首先是利用前面的程序生成迷宫矩阵matrix。
2、利用迷宫矩阵信息生成三维的图像
3、利用视角改变函数gluLookat不断的来改变视角,从而模拟走迷宫的场景
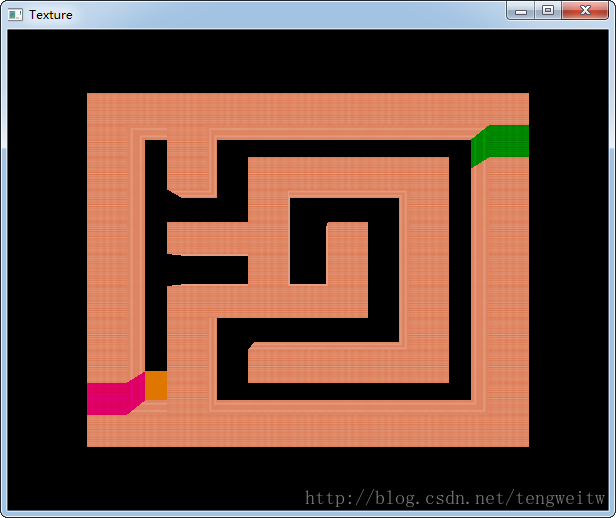
使用指南:
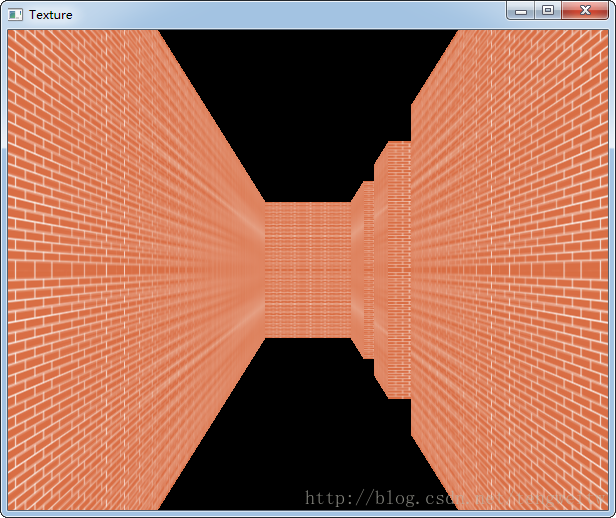
1、上下键控制前进、后退
2、左右键控制左转、右转
3、开始时,处于俯视图状态,可以看清地图的全貌以及自己在地图的位置(黄色)。
4、按下I键进入游戏模式,即可进行走迷宫,按下O键退出游戏模式,进入俯视图模式查看信息。
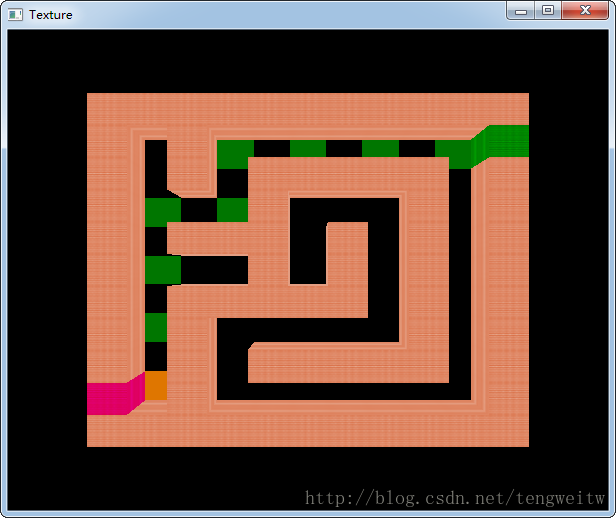
5、按p键,可以显示从入口到出口的可达路径(绿色)
6、分别用红色、绿色表示入口、出口
具体的显示效果如下:
1、初始情况(俯视图):
2、俯视图下显示可达路径:
3、游戏模式中:
4、游戏模式中显示可达路径:
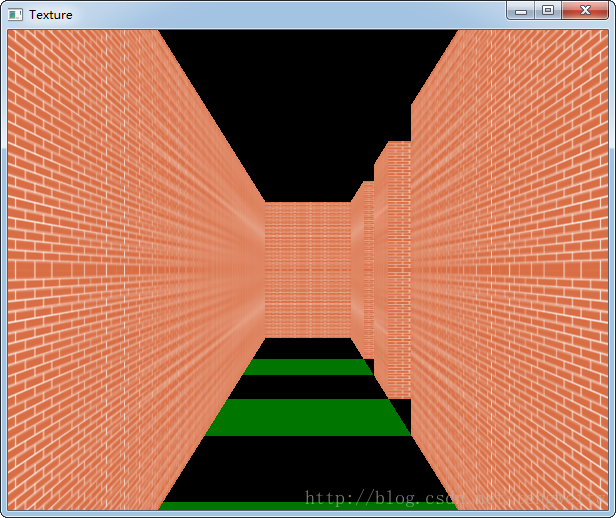
5、游戏模式转到俯视图查看当前位置:
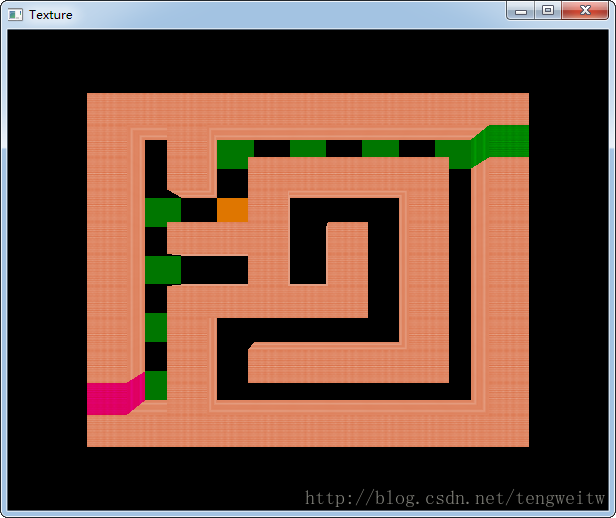
6、到达出口:
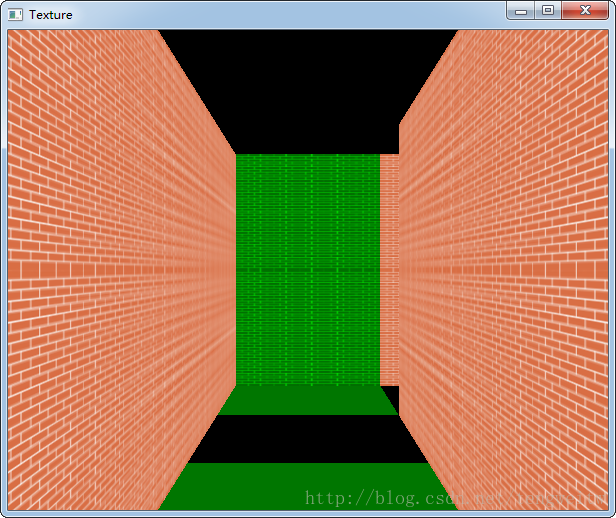
3D效果的不足之处:由于采用纹理轮廓不明显,导致转角处显示不明显,移动的步幅有点大,未经多次测试,可能存在bug。
由于篇幅有限,就不在此粘贴代码,具体源代码和可执行程序见下面链接:
http://download.csdn.net/detail/tengweitw/8154195
















